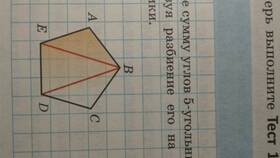
Сумма внутренних углов любого выпуклого многоугольника может быть вычислена по определенной математической формуле. Рассмотрим конкретный случай для двенадцатиугольника.
Содержание
Формула суммы внутренних углов
Для выпуклого n-угольника сумма внутренних углов (S) вычисляется по формуле:
S = (n - 2) × 180°
| Количество сторон (n) | Формула | Пример расчета |
| 12 | (12 - 2) × 180° | 10 × 180° = 1800° |
Доказательство формулы
Формула основана на разбиении многоугольника на треугольники:
- Из одной вершины проводим диагонали ко всем несмежным вершинам
- 12-угольник разбивается на 10 треугольников (n - 2)
- Сумма углов каждого треугольника равна 180°
- Общая сумма: 10 × 180° = 1800°
Графическая иллюстрация
| Количество треугольников | Сумма углов |
| 1 | 180° |
| 10 | 1800° |
Вычисление одного угла правильного 12-угольника
Для правильного двенадцатиугольника (все углы и стороны равны) величина каждого внутреннего угла (α) вычисляется:
α = S / n = 1800° / 12 = 150°
Свойства правильного 12-угольника
- Все внутренние углы равны 150°
- Центральный угол равен 30° (360°/12)
- Количество диагоналей: 54 (n(n-3)/2)
Сумма внешних углов
Для любого выпуклого многоугольника, включая 12-угольник, сумма внешних углов всегда равна 360° независимо от количества сторон.
| Тип углов | Сумма |
| Внутренние | 1800° |
| Внешние | 360° |
Практическое применение
Знание суммы углов 12-угольника используется в:
- Архитектуре и дизайне
- Геодезических расчетах
- Компьютерной графике
- Конструировании механических деталей