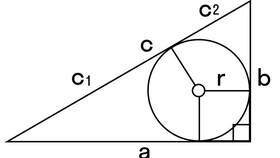
Площадь произвольного треугольника можно вычислить различными способами в зависимости от известных параметров фигуры. Рассмотрим основные формулы для расчета площади треугольников любого типа.
Содержание
Площадь произвольного треугольника можно вычислить различными способами в зависимости от известных параметров фигуры. Рассмотрим основные формулы для расчета площади треугольников любого типа.
Основные формулы площади треугольника
| Известные параметры | Формула |
| Основание и высота | S = ½ × a × h |
| Две стороны и угол между ними | S = ½ × a × b × sin(γ) |
| Три стороны (формула Герона) | S = √[p(p-a)(p-b)(p-c)] |
| Координаты вершин | S = ½|(x₂-x₁)(y₃-y₁)-(x₃-x₁)(y₂-y₁)| |
Пояснение к формулам
- a, b, c - длины сторон треугольника
- h - высота, проведенная к стороне a
- γ - угол между сторонами a и b
- p - полупериметр: p = (a+b+c)/2
- x₁,y₁; x₂,y₂; x₃,y₃ - координаты вершин
Примеры расчета площади
Пример 1: По основанию и высоте
Дано: a = 8 см, h = 5 см
Решение: S = ½ × 8 × 5 = 20 см²
Пример 2: По формуле Герона
Дано: a = 5 см, b = 6 см, c = 7 см
Решение:
- p = (5+6+7)/2 = 9
- S = √[9×(9-5)×(9-6)×(9-7)] = √[9×4×3×2] = √216 ≈ 14.7 см²
Особые случаи
- Для прямоугольного треугольника: S = ½ × катет × катет
- Для равностороннего треугольника: S = (a²√3)/4
- Для равнобедренного треугольника можно использовать любую из основных формул
Выбор формулы для расчета площади произвольного треугольника зависит от исходных данных задачи. Зная любые три элемента треугольника (из которых хотя бы одна сторона), можно определить его площадь.
